指导教师对本项目的支持情况指导教师为该项目的开展提供以下支持:
1、项目组成员组织协调上的支持:包括任务分配、人员变动、成果分配等。
2、项目经费使用上的监管:劳务费发放、数据收集费用支出等。
3、项目实施过程中技术上的指导:包括资料调研、建模设计、平台搭建、数据分析、论文撰写及投稿等。
4、项目实施过程中资源上的支持:包括实验室资源、校外资源(如企业、公司等)。指导教师对本项目的支持情况指导教师为该项目的开展提供以下支持:
1、项目组成员组织协调上的支持:包括任务分配、人员变动、成果分配等。
2、项目经费使用上的监管:劳务费发放、数据收集费用支出等。
3、项目实施过程中技术上的指导:包括资料调研、建模设计、平台搭建、数据分析、论文撰写及投稿等。
4、项目实施过程中资源上的支持:包括实验室资源、校外资源(如企业、公司等)。| 序号 | 学生 | 所属学院 | 专业 | 年级 | 项目中的分工 | 成员类型 |
|---|---|---|---|---|---|---|
|
|
陈心语 | 电气与动力工程学院 | 电气工程及其自动化 | 2022 | 统筹安排项目进度,整合申报书 |
|
|
|
苏鑫乐 | 电气与动力工程学院 | 电气工程及其自动化 | 2022 | 材料撰写 |
|
|
|
张喆 | 电气与动力工程学院 | 电气工程及其自动化 | 2022 | 数学分析 |
|
|
|
靖雅心 | 电气与动力工程学院 | 电气工程及其自动化 | 2022 | 材料撰写 |
|
|
|
费凡 | 信息科学与工程学院 | 通信工程 | 2022 | 编程、建模 |
|
| 序号 | 教师姓名 | 所属学院 | 是否企业导师 | 教师类型 |
|---|---|---|---|---|
|
|
梅飞 | 网络安全与信息化办公室、网络与信息技术中心(挂靠) | 否 |
|
当前,环境保护已经成为全球社会关注的焦点议题,在全球提倡加强环境保护和资源可持续利用的时代环境下,对储能系统的应用需求逐步增长。不同于其他种类电池,锂离子电池以其环境友好、比能量高、循环性能好、运行维修成本低、工作温度范围宽等特点被广泛应用于储能系统中,如笔记本电脑、移动电话、照相机、矿灯等便携式电子设备。因此,锂电池具有很好的应用前景,尤其是在航空航天领域。数据显示,受益于新能源汽车和动力电池,2016-2019年中国锂离子电池出货量逐年上升。根据高工锂电数据显示,2018年中国锂电池总出货量102GWh,同比增长27%。2019年中国锂离子电池出货量达到131.6GWh。2020年中国锂电池总出货量158.5GWh,同比增长20.4%。2020至2023年锂离子电池出货量也呈现快速增长,预计2024年中国的锂电池市场出货量将超过1100GWh,同比增长27%,正式进入TWh时代。
然而,近年来锂离子电池,尤其是车用动力电池安全事故频发,在一定程度上阻碍了新能源汽车等行业的发展。目前锂离子电池的安全性研究已经成为电池领域的研究热点。
事实上,锂离子电池组通常由成千上万节完全不一致的电池单体通过串并联的方式连接而成。由于生产过程中的缺陷、使用过程中的滥用操作以及电池的老化,每个电池单体或相关的组件都有可能出现各种故障,尤其是具有隐蔽性的短路故障和断路故障。同时锂离子电池具有强非线性和时变性的动态系统,其内部机理极其复杂,易受环境温度变化和电池老化的影响,导致故障诊断难度大,精度低。目前科学家和工程师们还无法有效评估或预测锂离子电池的安全性,因此,对锂离子储能系统进行健康状态评估,解决故障诊断难题,是提高储能系统安全性、可靠性和可用性的重要基础。
为此,本项目从锂离子电池电荷状态(State Of Charge,SOC)估计入手,研究锂电池内部机理与外部环境之间的关系,通过电流信号的矫正,提升SOC的自适应估计精确度;其次,考虑到外界干扰、测量误差、随机负载等因素影响,提取出锂电池组电压熵、平均温度和锂电池组健康状态(State Of Health,SOH)之间的映射关系,从而建立基于信息熵与PSO-LSTM的锂电池SOH估计模型;最后,分析各类故障数据,通过RBF神经网络与减聚类算法实现对锂离子电池的短路故障诊断。本项目旨在实现对锂离子储能系统的健康状态进行实时评估与故障诊断,以提高锂电池的安全性,可靠性和可用性,在未来的新能源汽车、航天航空等行业均有较好的应用前景。
1.典型锂离子电池的荷电荷状态(SOC)估计方法研究
荷电状态是电池管理系统(Battery management system,BMS)控制策略的典型判据之一,实时并准确地估计电池的SOC对储能设备的能量管理和功率分配控制以及产品的安全性具有重要意义。储能设备在工作时不可避免地受到干扰噪声的影响,具体表现为测量得到的电流和电压信号中掺杂有一定的随机噪声信号,如果将存在采样误差的电流或电压信号直接用于 SOC的估计中,则会造成估计精度的急剧下降甚至估计结果的发散。鉴于上述问题,本项目分析了不同类型以及不同强度的有色噪声形式,在电流信号受到有色噪声干扰而产生采样偏差的情况下,通过建立一种协同组合来估计结构实现电流信号在线校正、模型参数在线辨识以及 SOC的自适应估计。
2.典型锂离子电池健康状态(SOH)智能评估方法研究
为提高锂电池组SOH的估计精度,往往利用大量的数据构建锂电池组SOH估计模型。然而,在实际应用中,测量的数据往往受到干扰、测量误差、随机负载等未知因素的影响。为应对这一问题,本项目具体研究了一种基于信息熵与 PSO-LSTM 的锂电池组SOH估计方法,基于锂电池组恒流-恒压充电阶段锂电池组内各单体端电压的信息熵和平均温度信息,应用 PSO-LSTM 方法提取锂电池组电压熵、平均温度和锂电池组SOH之间的映射关系,从而建立锂电池组SOH估计模型。应用YXBP1000D多功能回馈式直流电子负载进行电池充电模拟,得出多组锂电池组老化数据并对提出的方法进行测试。利用美国航天航空局测得的锂电池加速老化数据再次测试,并与得出的实验结果进行误差分析,进一步验证项目的可行性。
3.典型锂离子电池短路故障诊断方法研究
神经网络是一种自学习自适应能力强,能够处理多输入多输出的非线性系统问题的有效方法。因此,采用RBF 神经网络进行故障诊断的研究,同时,利用减聚类算法进行相应的改进,把它们二者结合起来共同设计了锂离子电池故障诊断方案。本项目结合RBF神经网络的基本结构和减聚类算法的优势并针对动力电池单体故障,提出基于减聚类算法改进的RBF神经网络动力电池故障诊断方案。针对锂离子电池内短路故障诊断,构建基于Wasserstein测度的内短路故障特征距离矩阵,定量描述锂离子电池内短路故障,通过检测三维空间各点稀疏特性,衡量疑似故障电池偏离正常状态的程度,客观划定故障聚类,实现内短路故障检测。
1. 典型锂离子电池的荷电荷状态(SOC)估计方法研究
目前 SOC 估计的方法主要可分为四类:基于安时积分及其改进措施的方法[1];基于电池本征参数的映射估计方法,如开路电压(Open circuit voltage,OCV)法[2]、阻抗谱法等;基于数据驱动的方法,如人工神经网络法[3]、模糊逻辑法、支持向量机法[4]等;基于状态空间模型的方法,如卡尔曼滤波算法[5];基于改进粒子滤波的 LiFePO4 电池二元 SOC 估算[6]、滑膜状态观测器法[7]等。
安时积分法过分依赖初始 SOC 值的准确性和传感器的精度,易产生较大的累积误差。刘芳等[8]提出一种完全数据驱动的基于改进扩展卡尔曼滤波算法的电池全周期 SOC 估计方法,具有较好的鲁棒性,但卡尔曼滤波类算法的估计效果依赖模型的精度。ZHANG 等[9] 提出一种使用小波变换矩阵和自适应扩展卡尔曼滤波结合的 SOC 估计方法,基于小波阈值去噪的方法可以有效地对被污染的电流和电压信号进去分析和去噪,提高了 SOC的估计精度。
总而言之,现阶段所提出的采样信号校正方法忽视了噪声的多样性和复杂性,较少涉及到有色噪声的问题,使得估计算法在精度和鲁棒性等方面受到一定限制,无法适用于严苛工况。
2.典型锂离子电池健康状态(SOH)智能评估方法研究
为准确估计锂电池的健康状态,诸多方法被提出,目前主流的研究方法分为模型驱动的方法和数据驱动方法两大类。
(1)基于模型的方法本质上是建立电化学模型和数学模型来反映电池的实际运行状况。锂电池在使用过程中其内部的变量会随着工作时长的累积而发生改变,包括电池的电压、电流、阻抗以及温度等特征,通过对锂电池充放电历史数据做出分析与总结,建立合适的数学模型来反映锂电池的老化过程,以此来对锂电池的SOH做出预测。图1是目前主要几种基于模型的 SOH预测方法。
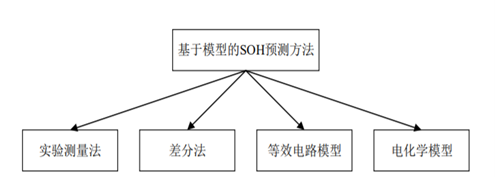
图1 基于模型的SOH预测方法
近年来,基于模型的预测方法取得了很大的进展,一些学者将模型的电阻和开路电压作为变量对电池的运行规律进行总结[10],也有学者通过分析电池失效机理,将电池的实际容量选定为反映电池健康度的主要因素,通过正态分布建立数学模型[11],对电池的运行状态进行统计分析,选取不同的阈值作为电池容量失效点以此来对电池容量和寿命做出预测。还有学者通过使用粒子滤波和卡尔曼滤波方法来辅助模型做出预测[12]。然而基于模型的预测方法也存在缺陷,在实际的操作中有着一定的局限性。模型在使用过程中,各个相关参数会出现细微的误差,而随着时间的推移,累计的误差没有得到校正与消除会导致预测结果出现偏差。另一方面,锂电池的容量回升现象和等效电路模型参数会发生非线性的变化问题使得基于模型的预测方法受到了一定的限制。基于模型的方法无法反映电池老化时的非线性变化问题,因此模型在模拟电池的运行规律和容量衰减状况 时与实际的电池老化情况有所不同,从而导致预测结果出现偏差。然而,在某些特定的场合下,基于模型的预测方法仍具有一定的可行性。
(2)数据驱动方法指的是采用高斯过程回归或机器学习的方法,深入探索电池的寿命衰减行为,通过训练电池退化数据集,寻找电池老化因子作为性能指标,建立电池的老化模型。20 世纪 80 年代以来,机器学习在全世界范围蓬勃发展,并开启在工业中的应用时代。2004 年,Chau 等人[13]提出了一种新的模糊神经推理模型估计电动汽车锂离子电池的剩余容量。通过将模型估计的电池的剩余容量与实验结果作比较,验证了该模型具有较高的精度。近年来,采用机器学习方法对电池老化模型进行回归的研究蓬勃发展。Liu等人[14]提出了一种考虑电池老化趋势以及相应的工作温度和放电深度的模型结构,在高斯过程回归的协方差函数的基础上,建立了两个相关的数据驱动模型,该模型可用于各种循环工况下的电池容量预测。此外,长短时记忆神经网络(Long short-term memory neural network, LSTM)作为一种循环神经网络,能够维持梯度不消失[15]且长时间有效地存储和更新信息,因此常被用来估计锂电池健康状态,但是对于如何设置 LSTM 最佳的学习率并没有合适的方法。
3.典型锂离子电池短路故障诊断方法研究
目前,针对动力电池的故障诊断问题,国内外学者做了大量研究,提出了多种方法,通常按照是否需要电池模型分为两个大类:基于模型的故障诊断方法和无模型的故障诊断方法。
(1)基于模型的故障诊断方法:该方法基于常见的动力电池模型,比如电化学模型、热模型、电热模型和电路模型等,并结合参数估计、状态估计等方法进行故障诊断。这种方法最重要的是要建立准确牢靠的动力电池模型,通过计算分析实际测量值与电池模型预测值的区别来进行故障诊断。[16]建立了一种基于两层结构的电池外短路故障模型,根据实验结果,外短路故障在5s内得到诊断,且实测数据与故障模型误差小于0.36V。[17]同样建立了电池外短路故障模型,采用遗传算法进行模型参数辨识,提出了一种三步诊断算法,几个例子都证实了算法的可行性。[18]提出一种基于累积和(cumulative sum,CUSUM)事件段检测与改进谱聚类的锂离子电池储能系统内短路故障检测方法。[19]针对电池内短路故障,建立均值差异模型,运用递归最小二乘法进行模型参数估计,实验表明,该方法可以有效检测短路电阻,实现对内短路故障的诊断。
(2)无模型的故障诊断方法:该方法无须建立动力电池的动态特性模型,可以省去建模的复杂度以及参数估计的更新计算,但更加依赖样本数据质量,通常又可以细分为基于知识的方法和基于数据驱动的方法。基于知识的故障诊断方法运用各种规则、理论、知识库、专家经验等作为参照,对比实时电池数据进行推理判断,实现故障的检测与分类。[20]根据电池专家的故障诊断经验结合模糊理论建立了动力电池故障诊断专家系统,通过电池状态数据运用专家系统正向推理得到故障分类结果。此外,故障树分析法也常常用于动力电池故障诊断中,[21]发挥了故障树分析法、模糊理论的优点,建立了模糊故障树用于汽车故障诊断。基于数据驱动的故障诊断方法通过采集电池系统运行过程中的实时数据,运用各种理论方法进行分析处理来对故障数据进行鉴别和分类。这些技术手段主要包括机器学习与数据挖掘方法、信号处理方法、统计分析法等。[22]运用BP神经网络和RBF神经网络对锂电池多个故障进行了诊断和分类。[23]研究了电池短路故障造成的温升问题,提出了一种基于支持向量机的故障温升在线预测方法。[24]则是利用数学中相关系数的方法分析电池电压数据,分别实现了短路故障、电压故障和多种故障的诊断。随着人工智能、数据挖掘、机器学习等技术的发展,运用基于数据驱动的动力电池故障诊断方法越来越广泛。
参考文献:
[1] 罗勇,祁朋伟. 基于容量修正的安时积分 SOC估算方法研究[J]. 汽车工程,2020,42(5):681-687.
[2] LEE S J,KIM J H,LEE J M,et al. The state and parameter estimation of an li-ion battery using a new OCV-SOC concept[C]//Orlando,FL,United States:Institute of Electrical and Electronics Engineers Inc., 2007:2799-2803.
[3] 李超然,肖飞,樊亚翔,等. 基于深度学习的锂离子电池 SOC 和 SOH 联合估算[J]. 中国电机工程学报,2020, 10(8):1-13.
[4] 王语园,李嘉波,张福. 基于粒子群算法的最小二乘支 持向量机电池状态估计[J]. 储能科学与技术,2020, 9(4):1153-1158.
[5] 熊瑞,李幸港. 基于双卡尔曼滤波算法的动力电池内部 温度估计[J]. 机械工程学报,2020,56(14):146-151.
[6] 燕山大学学报,2019,43(6):511-517.
[7] 高铭琨,徐海亮,吴明铂. 基于等效电路模型的动力电 池 SOC 估计方法综述[J]. 电气工程学报,2021,16(1):90-102.
[8] 刘芳,马杰. 基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J]. 电工 技术学报,2020,35(4):699-707.
[9] ZHANG Z,CHENG X,LU Z,et al. SOC estimation of lithium-ion batteries with AEKF and wavelet transform matrix[J]. IEEE Transactions on Power Electronics,2017,32(10):7626-7634.
[10] 张持健, 陈航. 锂电池 SOC 预测方法综述[J]. 电源技术, 2016, 40(6):4-6.
[15] ZHANG Y,XIONG R,HE H, el al. Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries[J]. IEEE Transactions on Vehicular Technology,2018,67(7):5695-5705.
[16] Chen Z, Xiong R, et al. Applied Energy, 2016, 184:365-374.
[17] J. Journal of Cleaner Production, 2018, 187: 950-959.
[18] 肖先勇;陈智凡;汪颖;何涛;张逢蓉;,基于累积和事件段识别与改进谱聚类的锂离子电池储能系统内短路故障检测方法,[J],电网技术,2024,13,13
[19] Gao W, Zheng Y, Ouyang M, et al. 2019, 66(3): 2132-2142.
[20] 刘文杰,齐国光.基于模糊理论的电池故障诊断专家系统[J] .吉林大学学报(信息科学版),2005,23(6):670-674.
[21] 夏淑英.基于模糊故障树的汽车故障诊断方法及其应用研究[D].武汉:湖北工业大学,2017.
[22] 古昂,张向文.基于 RBF 神经网络的动力电池故障诊断系统研究门.电源技术,2016,40(10): 1943-1945.
[23] Chen Z, Xiong R, et al. [J]Applied Energy, 2018, 213:375-383.
[24] Xia B, et al. [J]Journal of Power Sources, 2017, 337: 1-10.
1. 典型锂离子电池的荷电荷状态(SOC)估计方法研究
该方案的创新点在于考虑了电流信号受有色噪声污染形式下的 SOC 估计问题,所提出的三层组合估计结构在电流信号被严重破坏的情况下,仍能实现电池模型参数的在线辨识和 SOC 的高精度在线估计。
2.典型锂离子电池健康状态(SOH)智能评估方法研究
与传统的直接测量、模型驱动估算锂电池SOH的方法相比,该方案大大减少了在实际应用中,测量的数据受到干扰、测量误差、随机负载等未知因素的影响。提高锂电池组SOH的估计精度,能够准确估计锂电池组SOH。
3.典型锂离子电池短路故障诊断方法研究
该方案针对电池单体,提出运用人工神经网络进行故障诊断的思路,结合减聚类算法的优点,进一步提出了基于改进的RBF神经网络动力电池故障诊断方案,设计了故障诊断流程,该诊断方案可实现电池单体的故障诊断,且比传统的RBF神经网络诊断精度更高,速度更快。
1. 典型锂离子电池的荷电荷状态(SOC)估计方法研究
本项目分析了不同类型以及不同强度的有色噪声形式,在电流信号受到有色噪声干扰而产生采样偏差的情况下,通过建立一种协同组合估计结构实现电流信号在线校正、模型参数在线辨识以及SOC 自适应估计。该组合结构首先基于状态扩维后二阶RC等效电路模型,并利用自适应重组遗传算法(Adaptive recombination genetic algorithm,ARGA)辨识出模型参数,由自适应平方根容积卡尔曼滤波(Adaptive square root cubature Kalman filter,ASRCKF)算法在线校正产生偏差的电流信号;然后基于校正后的电流信号和二阶RC模型,通过偏差补偿遗忘因子递推最小二乘 (Bias compensation recursive forgetting-factor least squares,BCFRLS) 算法与 ASRCKF 算法相结合进行协同估计,实现模型参数和SOC值的在线更新。
其具体技术路线如下:
1.1二阶RC等效电路模型建模
动力锂离子电池的内部反应复杂,其参数具有很强的时变性和非线性。为了能够准确描述电池在不同时间尺度下的电压变化规律,综合考虑模型的准确性和运算的复杂性问题,本文选取二阶 RC 等效电路模型进行电池建模,模型结构如图 2所示
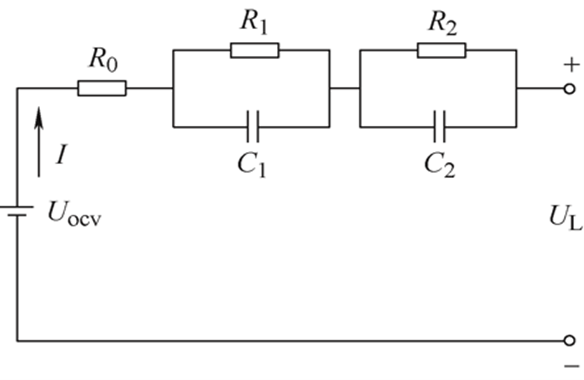
图2 二阶RC等效电路模型
在图 2 中,UOCV表示电池的开路电压, UL表示电池的端电压, R0表示电池的欧姆内阻, R1和R2表示 极化电阻,C1和C2表示极化电容,I表示电池的干路电流,并在此规定放电时电流方向为正,反之为负。
当电流信号中掺杂有色噪声信号时,传统的二阶RC模型便不能真实地反映电池的外部特性,从而造成基于模型的 SOC 估计精度下降。鉴于此,对二阶 RC 模型的状态空间进行改进,将电流偏差量引入到状态空间模型。则扩维后的状态空间模型的状态量变为![]()
设电流传感器的测量值为Is ,电流偏差量为Ib, 则电流信号的真实值I可表示为


基于改进的模型可以实时在线估计电流偏差量 从而修正电流信号,提高电池模型的准确性。
1.2 BCFRLS 算法参数辨识
(1) 在进行在线辨识运算前,需要对电池模型进行相应转化,处理方式如下:
根据电池模型的时域关系式,通过拉氏变换,并以干路电流真实值作为系统输入,内部阻容电压为输出,得到电池模型的频域关系式
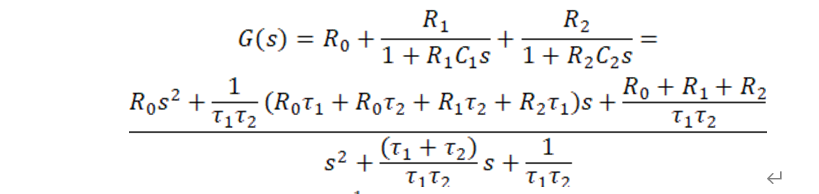
采用双线性变换,令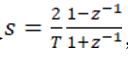 将传递函数进行离散化处理,以实现由复频域到离散域的转换,
将传递函数进行离散化处理,以实现由复频域到离散域的转换,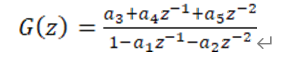
其中,![]() 为待定系数
为待定系数
将式子转换成差分方程的形式,并转换成矩阵形式![]()
在线辨识算法中,通过递推运算,便可在每个 采样点处更新待辨识的参数。
(2) 在线辨识算法中,电压信号作为观测值参与运算,而在相同的噪声强度下,电压信号的准确性对模型精度的影响更大,因此本文针对仅电压信号中掺杂有零均值的高斯白噪声时,提出相应的偏差补偿方式。
1.3基于 ASRCKF 算法的电池状态估计

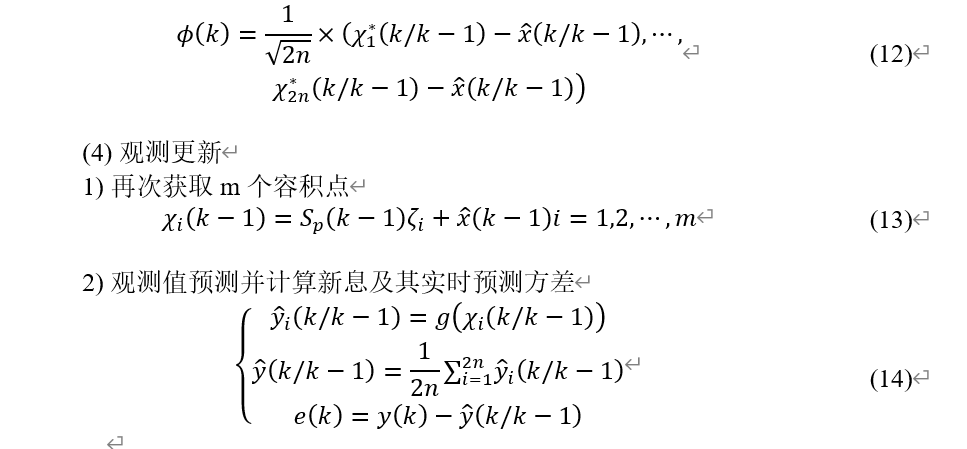
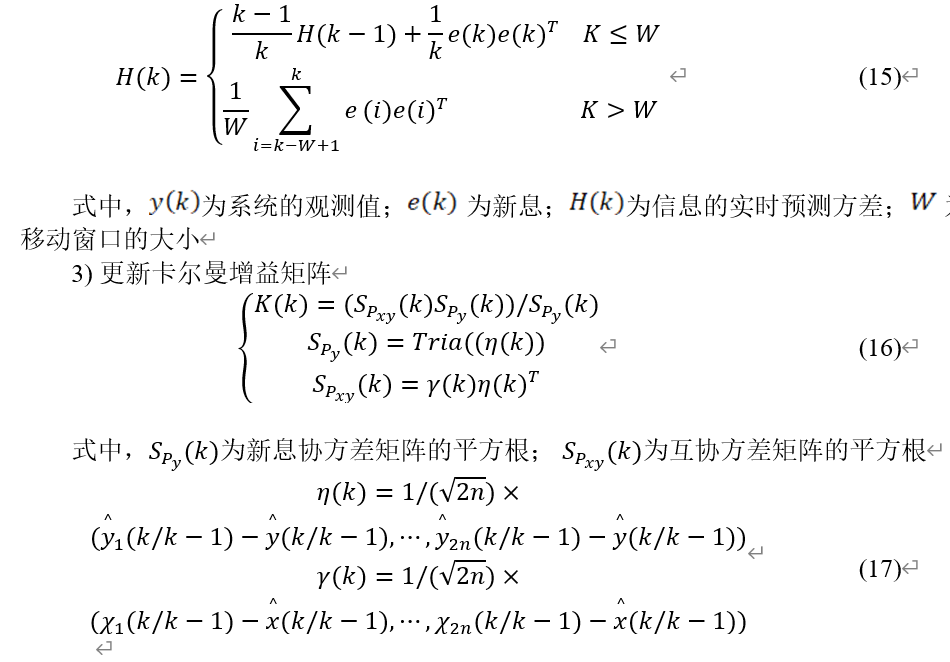

1.4基于三层组合结构的SOC估计
提出一种三层组合协同估计结构,在电流信号中包含色噪声时,可同时实现电流信号校正、模型参数在线辨识和 SOC 估计,该结构如图
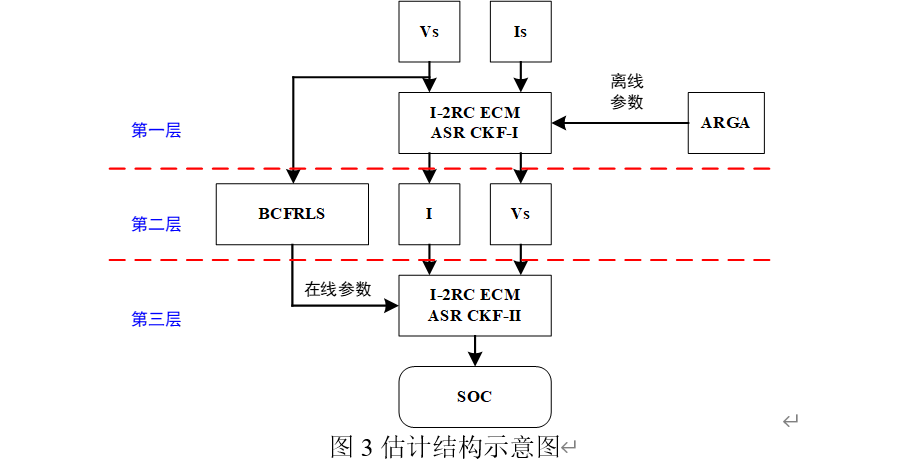
在该三层组合估计结构中,其输入为 BMS传感器测量得到的电流信号Is和电压信号Vs,其中,流信号中含有有色噪声信号,而假设电压信号中只含有高斯白噪声信号,结构域的输出为 SOC 的估计值。第一层结构仅用于修正电流信号,ASRCKF 算法基于由 ARGA 辨识的状态扩维的二阶 RC 模型,在 和 的驱动下,通过递推计算输出电流的修正值 ,并输入到第二层结构中;第二层结构用于模型参数的在线辨识,其输入不再是原电流信号,而是经第一层结构修正后的电流信号,通过BCFRLS 算法实时更新模型参数,并输入到第三层 结构中;第三层结构用于在线估计电池 SOC,在此层结构中采用在线二阶 RC 模型,通过 ASRCKF 算法最终实现 SOC 的高精度估计。
具体步骤:
(1) 初始化BCFRLS算法和ASRCKF算法的各项初始值。
(2) 基于ARGA辨识得到的参数构建二阶RC等效电路状态空间模型。
(3) 通过电流和电压数据,启动第一层下的ASRCKF 算法,估计电流偏差量,校正电流信号。
(4) 通过电压数据和修正的电流数据,启动第三层 ASRCKF 算法,估计 SOC。
(5) 利用 SOC 的后验估计值和 OCV-SOC 关系,输出 OCV 的后验估计值。
(6) 通过第一层输出的电流数据、电压数据以及OCV 的估计值,启动 BCFRLS 算法,辨识模型参数。
(7) 辨识参数输入 ASRCKF 算法,估计 SOC。通过步骤 (3)~(7)的循环递推计算,即可实现SOC值的估计。
2.典型锂离子电池的荷电状态(SOH)的研究
2.1基于信息熵与PSO-LSTM的锂电池组健康状态评估
为提高锂电池组健康状态的估计精度,往往利用大量的数据构建锂电池组健康状态估计模型。然而,在实际应用中,测量的数据往往受到干扰、测量误差、随机负载等未知因素的影响。为应对这一问题,提出一种基于信息熵与PSO-LSTM 的锂电池组健康状态估计方法。利用恒流-恒压充电阶段的锂电池组内各单体电压熵和平均温度有效地反映电池容量退化,进一步利用 PSO 算法改进的 LSTM 神经 网络获取锂电池组电压熵、平均温度和健康状态之间的映射关系,建立锂电池组健康状态估计模型,从而对锂电池组健康状态精准估计。由于锂电池组的健康状态随着不断地充放电而退化,故可以将锂电池组健康状态的退化过程视为时间序列过程,它可以覆盖数千次充放电循环,代表锂电池组的退化演化。故锂电池组历史运行数据与其健康状态存在长期依赖关系,因此采用时间序列分析方法 LSTM 神经网络,采集锂电池组不同充放电次数的充电阶段的电压熵与温度数据,估计其对应放电阶段的健康状态。
2.2算法参数介绍
(1)锂电池健康状态
锂电池组健康状态可以从容量和内阻两个角度 进行定义,定义式可表示

由于容量定义法更为精确且参量容易获取。因此,以容量的角度对锂离子电池组健康状态进行定义。
(2)信息熵
由于信息熵主要依赖于概率分布,因此可以更好地表征数据的不确定性,并有效地反映数据所携带的信息量。信息熵越低,数据的有序度越高。反之,信息熵越高,说明数据所携带的信息是分散的。信息熵定义为

式中, 为第 个样本采样点的概率, 为表示所有采样点数目的总数。
准确估计锂电池组健康状态通常需要大量的数据建立锂电池组健康状态估计模型,但实际测量的数据往往包含各种噪声。基于含有噪声的数据估计,锂电池组健康状态会产生较大的误差且直接提高估计难度。因此,需要对原始数据进一步处理,提取有效特征。经过多次尝试发现,利用信息熵量化电池数据的规律性和不确定性,提取原始数据中的有效特征,每个充电阶段将成百上千个采样电压化为一个电压熵值,即可以有效降低对实际应用的计算 复杂度,又能够很好地映射锂电池组退化过程。
(3)PSO-LSTM
1.LSTM神经网络
LSTM 神经网络是一种循环神经网络,常见的循环神经网络结构如图4示。其中,x为输入,h为输出,t为时间,w、u、v为网络参数。
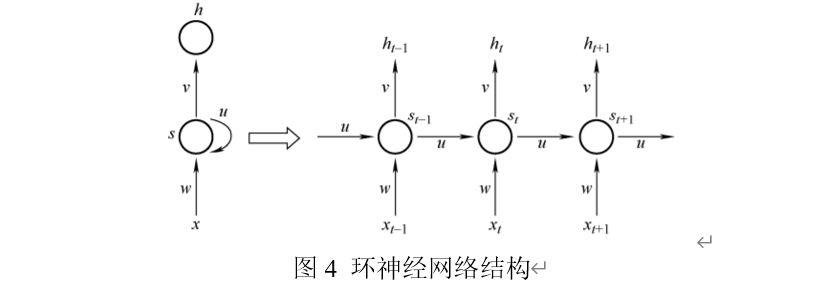
可以看出,隐含层的输出中带有当前的信息状态,作为下一层的输入被传递到下一个隐含层。这一显著特征保留前一步的信息,从而提高循环神经网络对时间序列问题的学习能力。然而,对于长期依赖问题,循环神经网络存在梯度消失现象,导致数据信息不能远距离转移。对于循环神经网络的梯度消失问题,目前最有效的解决方案是 LSTM 神经网络。LSTM 神经网络的设计关键是将非线性和数据相关的控制单元纳入循环神经网络单元,循环神经网络单元可以经过训练,以确保与状态信号相关的目标函数的梯度不会消失。
LSTM 神经网络基本结构如图5所示。显然,LSTM 神经网络隐含层的内部结构比循环神经网络更为复杂。LSTM 神经网络主要包括存储单元、遗忘门、输入门和输出门。遗忘门可以丢弃多余的信息,输入门能够选择要存储在内部状态的关键信息,输出门用于确定输出信息。利用记忆单元的状态,借助三门选择性地添加或删除信息。因此,LSTM 神经网络可以在长时间内有效地存储和更新关键信息,而不会出现梯度消失的情况。
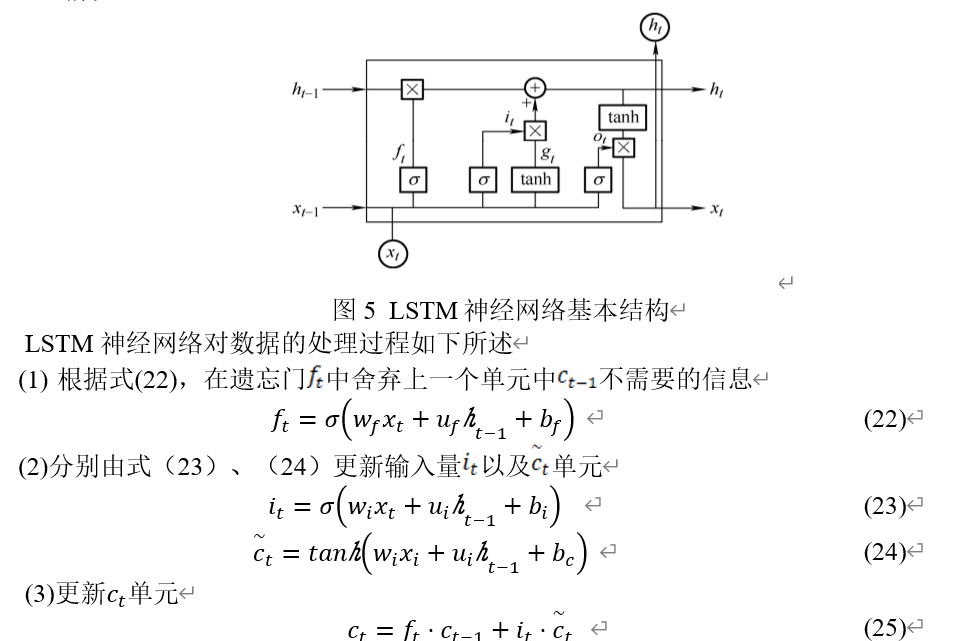

学习率作为 LSTM 神经网络的重要超参数,控制着模型的学习进度,决定目标函数是否以及何时收敛到最优解。适当的学习率可以使目标函数在适当的时间内收敛到最优解。但学习率较大容易导致算法输出振荡,学习率较小则会造成过拟合和收敛缓慢。因此,对于 LSTM 神经网络,合适的学习率非常重要。故采用 PSO 算法优化 LSTM 神经网络的学习率。
2.PSO算法
粒子群优化算法是一种基于群体搜索的全局优化算法。它是受鸟类群集或鱼类群集的启发而开发,用于解决许多科学和工程领域优化问题。PSO 算法通过定义的适应度函数,不断更新粒子的速度和位置从而达到全局最优解。粒子群算法在 D-维空间中寻优的基本流程为:

2.3 PSO 算法优化 LSTM 神经网络
采用平均绝对误差作为适应度函数,即锂电池组健康状态估计值与真实值间的误差作为适应度函数。PSO 优化 LSTM 神经网络学习率的步骤具体描述为:
(1) 初始化 PSO 算法参数,如群体规模、粒子 指标、迭代次数、粒子速度和位置、结束条件等。同时,根据经验设置 LSTM 神经网络的学习率范围。
(2) 根据适应度函数计算每个粒子的适应度值。
(3) 将每个粒子的当前适应度值与其历史适应度值进行比较,生成每个粒子的局部最优解。将粒子当前的适应度值与所有历史适应度值进行比较,得到全局最优解。
(4) 分别用式(34)和式(35)更新每个粒子的速度和位置。
(5) 重复步骤(2)~(4),直至达到算法终止条件。
(6) 输出 PSO 算法优化后的 LSTM 神经网络学习率
具体步骤如下:
(1) 根据恒流-恒压充电阶段锂电池组内各单体电池端电压与温度变化数据,计算每次恒流恒压充电阶段锂电池端电压数据的信息熵、平均温度与每个放电阶段后的健康状态数据,生成处理后的数据集。
(2) 将处理后的数据集均分为训练集和测试集。
(3) 基于训练数据,使用 PSO 算法对 LSTM 神经网络预处理,对 LSTM 神经网络的学习率进行优化选择。
(4) 应用 PSO 算法优化获得的学习率,基于优化后的长短时记忆神经网络建立锂电池组健康状态估计模型。
(5) 应用建立锂电池组健康状态估计模型,基于测试数据估计锂电池组的健康状态。
3.典型锂离子电池短路故障诊断方法研究
动力电池故障种类多,故障诱发原因复杂,多种故障还可能并发产生,神经网络是一种自学习自适应能力强,能够处理多输入多输出的非线性系统问题的有效方法。因此,采用RBF神经网络进行故障诊断的研究,同时,利用减聚类算法进行相应的改进,把它们二者结合起来共同设计了动力电池单体故障诊断方案。除此之外,针对内短路故障的检测问题,提出一种基于CUSUM事件段识别与改进谱聚类的锂离子电池储能系统内短路故障检测方法,构建基于Wasserstein测度的内短路故障特征距离矩阵,通过检测三维空间稀疏特性,实现基于改进谱聚类的内短路故障单体检测。
3.1 RBF神经网络
人工神经网络是人工智能技术的研究热点,其在模式识别、控制与优化、图像处理、医学、经济、智能机器人等领域取得了诸多良好的成果。RBF神经网络的网络拓扑结构如图6所示,它由输入层、径向基函数隐含层、输出层三层组成,是一种前馈式神经网络。输入层只负责接受输入信号,而不对其进行处理,它们起到神经网络内部和外部连接的作用。本节设计的动力电池故障诊断系统中的输入信号包括电池电压、电池温度、SOC、电池内阻、容量等。
输入信号从输入层传递到隐含层,隐含层利用其中的径向基函数实现从输入层到隐含层的非线性变换。高斯函数曲线光滑,任意阶导数都存在,且形式简单,便于理论分析,就成为了RBF神经网络中最常用的径向基函数,本文中隐含层神经元的基函数也选用高斯函数:
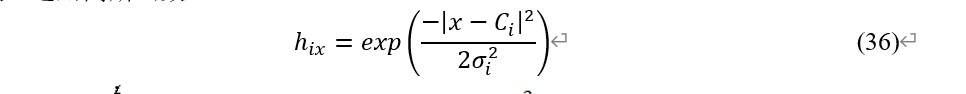
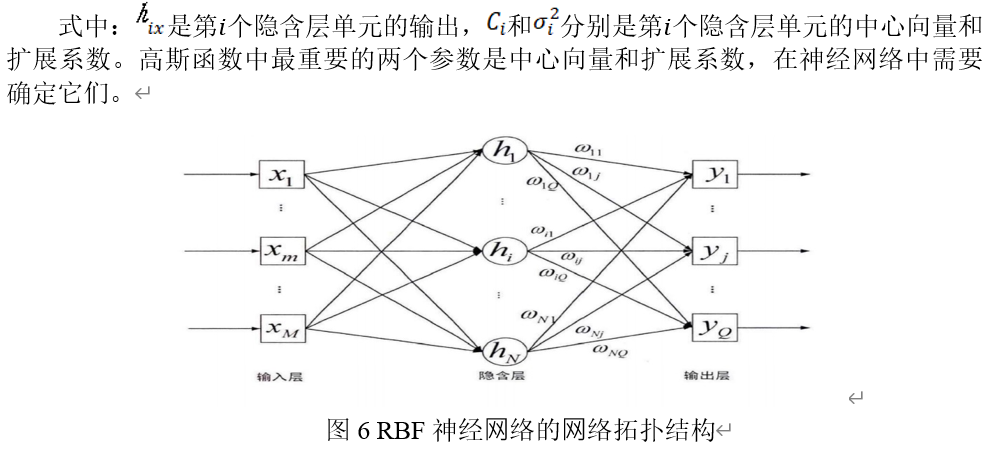
来自隐含层的信号在输出层要进行线性变换,输出层的输出信号是对输入信号进行加权线性求和得到,输出层的输出为:

从总体上看,RBF神经网络的输入与输出之问是非线性的,但输出对权值向量又是线性的,因此非线性不可分问题就成为了一个线性可分问题,并通过线性单元来解决。它可以逼近任意的非线性函数,能够处理复杂的系统问题而不需要找到其中的规律性,并且具有很快的学习收敛速度,因此RBF神经网络有广泛的应用。
3.2 减聚类算法
减聚类算法(Subtrative Clustering Method,SCM)是一种基于密度的聚类算法,它是一种简单而又相对有效的聚类算法的,与一般的聚类算法需要提前确定聚类数不同,减聚类算法不用提前确定聚类的数目,而是把所有的输入样本都作为聚类中心的候选,然后通过各数据点的密度指标来我到所行的聚类中心。减聚类算法的流程如图7所示。
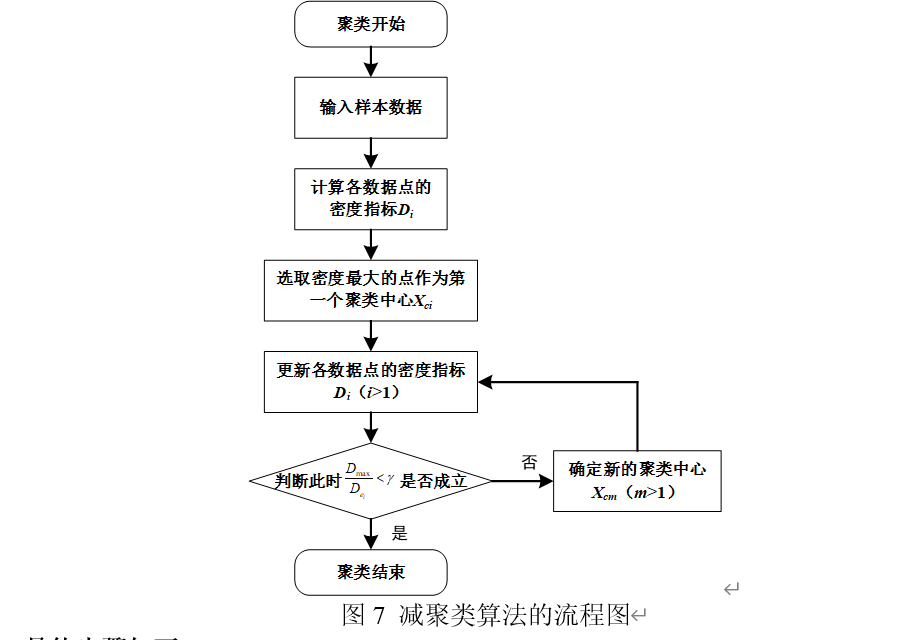


确定了聚类中心之后,取聚类中心与其近邻的数据点间的平均距离作为扩展系数聚类算法的目标是使簇间数据样本之间相距尽可能大,簇内数据样本之间相距尽可能小,通过以上算法过程的描述,我们看出减聚类算法很好的满足了这一目标。
3.3wasserstein测度
基于Wasserstein测度定量描述各单体与安全基准的三维故障特征相似程度。以单体1和单体M的电压偏差特征S1、SM为例,Wasserstein距离越大,表明2个序列的相似度越低,也即是偏离安全基准的距离越大,存在故障的可能性越高。进行Wasserstein距离计算时,可将S,视为一座有q-d个站台的出发点,从内部第m个站台出发,到达SM1的第n个站台的距离为

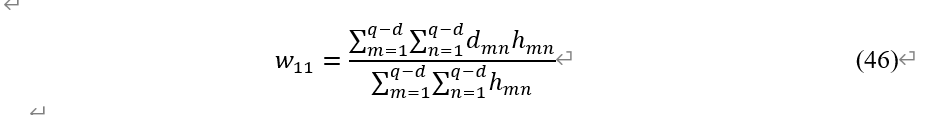



2024年4月至2024年6月,小组成员根据自身不同的分工,进行Python、MATLAB语言、数学建模及相关知识的学习,并继续大量阅读文献。
2024年7月至2024年9月,进行电流信号采样偏差下动力电池荷电状态、信息熵与PSO-LSTM的锂电池组健康状态、基于减聚类算法的RBF神经网络动力电池故障以及Wasserstein测量的内短路故障程序系统设计,通过Python、MATLAB建立起系统模型,并不断完善,得到一个较为完善的结果。
2024年10月,基于SOC、SOH和短路故障分析研究结果,争取投出一篇专利和一项软件著作权。
2024年11月至2025年1月,利用YXBP1000D设备进行数据模拟测试,得到数据并通过所设计的软件呈现出来。
2025年2月至2025年3月,进行软件功能测试并且进行调试,确保项目能稳定地实现所设计的功能。完成论文初稿。
2025年4月至2025年5月,对系统进行全面的测试,及时发现系统所存在的问题并进行修改,不断优化系统的细节,确保系统的稳定运行。同时对项目进行总结与反思,完善项目论文,并最终完成结题工作
项目申报团队在指导教师的帮助下已具备以下研究基础:
目前有大量锂离子储能系统SOC、SOH评估和故障分析研究的论文可供借鉴。
团队成员目前均学习过计算机编程原理,部分成员已经掌握了Python编程基础。
团队成员目前在队长的组织下展开过多次研讨,对项目开展思路与团队分工非常明确,团队执行力强。
指导教师所在的江苏省配用电与能效工程技术研究中心为项目的开展提供了可靠的软硬件实验条件,以及丰富的数据来源。
已具备的条件:
①在上述电池短路故障诊断所需要的实测数据可以从电⽹公司得到,模拟参数可以从电池模拟柜得到。
②校图书馆和图书馆网站提供丰富的纸质资料和电子资料,覆盖面广,具有较强的时效性和权威性,提供了大量的资料支撑。
③学校通过指派导师对本小组进行指导和监督,督促本小组成员在规定时间内完成任务并且进行指导。
④学校支持学生积极参与到创训中来,并且为项目的顺利开展提供经费支持。
实验条件:
江苏省配用电与能效工程技术研究中心配置了YXBP1000D型电池模拟器,可以为项目顺利进行提供必要数据支持。




图8 电池模拟器及操作界面
YXBP1000D电池模拟器能够模拟各种电池的充放电特性。主要场合为微电网储能系统、PCS(储能逆变器)、电动汽车双向充电机的测试和电池组充放电等。具备模拟多种电池的充放电的特性,用户可选择模拟不同电池的类型、串联 节数、并联节数及SOC 指标,从而全面模拟电池的输出特性,包括了电池放电过程中电池内阻特性变化的过程。
| 开支科目 | 预算经费(元) | 主要用途 | 阶段下达经费计划(元) | |
|---|---|---|---|---|
| 前半阶段 | 后半阶段 | |||
| 预算经费总额 | 1500.00 | 无 | 1000.00 | 500.00 |
| 1. 业务费 | 1500.00 | 无 | 1000.00 | 500.00 |
| (1)计算、分析、测试费 | 0.00 | 无 | 0.00 | 0.00 |
| (2)能源动力费 | 0.00 | 无 | 0.00 | 0.00 |
| (3)会议、差旅费 | 0.00 | 无 | 0.00 | 0.00 |
| (4)文献检索费 | 0.00 | 无 | 0.00 | 0.00 |
| (5)论文出版费 | 1500.00 | 无 | 1000.00 | 500.00 |
| 2. 仪器设备购置费 | 0.00 | 无 | 0.00 | 0.00 |
| 3. 实验装置试制费 | 0.00 | 无 | 0.00 | 0.00 |
| 4. 材料费 | 0.00 | 无 | 0.00 | 0.00 |